Frustum
A frustum is the portion of a solid that lies between two parallel planes cutting it. A right frustum is a parallel truncation of a right pyramid.
Formulae used
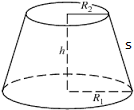
h = height of frustum
s = slant height
R2 = small-radius of frustum
R1 = big-radius of frustum
\[Volume \: of frustum\: \: =\: \frac{\pi }{3}h\left ( R_{1}^{2} +R_{2}^{2}+R_{1}*R_{2}\right ) \]
\[s = \sqrt{\left (R_{2}-R_{1} \right )^{2}+h^{2}} \]
\[Lateral \: surface \: area = \pi s\left ( R_{1} +R_{2}\right ) \]
\[Top\: surface\: area(T) = \pi R_{2}^{2} \]
\[Base\: surface\: area(B) = \pi R_{1}^{2} \]
\[Total \: surface\: area =\pi \left ( R_{1} + R_{2}\right )l + \pi R_2 ^2 +\pi R_1^2 \]