Equations of motion: Position-time
The displacement of a moving object is directly proportional to both velocity and time.
Derivation:
Let's start with the definition of velocity in order to derive this equation
\[\overline{v} = \frac{\Delta s}{\Delta t} \]
Expand Δs to s − s0 and condense Δt to t.
\[\overline{v} = \frac{s - s_{0}}{t} \]
Solve for position.
\[s = s_{0} + \overline{v}t -->(1) \]
When the rate of change of a quantity is constant, the quantity changes at a uniform rate so that its average value is halfway between its initial and final values.
\[\overline{v}= \frac{1}{2}\left ( v + v_{0} \right ) --> [a] \]
Substitute the first equation of motion ( \[v = v_{0} + at \] ) into this equation [a] and simplify with the intent of eliminating v.
\[\overline{v} = \frac{1}{2}\left [ \left ( v_{0} + at \right ) + v_{0} \right ] \]
\[\overline{v} = \frac{1}{2}\left [ 2v_{0} + at \right ] \]
\[\overline{v} = v_{0} + \frac{1}{2}at --> (2) \]
Substitute (2) into (1) to eliminate 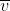
\[s = s_{0} + (v_{0} + \frac{1}{2}at)t \]
And finally, solve for s as a function of t.
\[s = s_{0} + v_{0}t + \frac{1}{2}at^{2} \]