Magnetic field
A magnetic field is a picture that we use as a tool to describe how the magnetic force is distributed in the space around and within something magnetic.
Magnetic fields are produced by electric currents, which can be macroscopic currents in wires, or microscopic currents associated with electrons in atomic orbits.
he magnetic field lines form concentric circles around the wire. The magnetic field direction depends on the direction of the current. It can be determined using the "right hand rule", by pointing the thumb of your right hand in the direction of the current. The direction of the magnetic field lines is the direction of your curled fingers. The magnitude of the magnetic field depends on the amount of current, and the distance from the charge-carrying wire. The formula includes the constant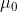 
. This is called the permeability of free space, and has a value \[\mu _{0}=4\pi \times 10^{-7}(T.m)/A \] . The unit of magnetic field is the Tesla, T.
\[magnetic\; field \; magnitude = \frac{\left ( permeabilty\: of \: free\: spcae \right )\left ( current\: magnitude \right )}{2\pi\left ( distance \right )} \]
\[B=\frac{\mu _{0}I}{2\pi r} \]
B = magnetic field magnitude (Tesla, T)
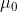= permeability of free space (\[4\pi\times 10^{-7}T.m/A \])
I = magnitude of the electric current (Amperes, A)
r = distance (m)
